Lots of the Google Apps Script projects that people are working on start with a Google Spreadsheet as a base. Sometimes a Google Form writes data to a spreadsheet that triggers other events, or you have a Sheet you’ve imported that you want to use to coordinate a larger workflow.
This post will describe different ways of getting row data from a Google Sheet using Google Apps Script, and then walk you through ways to process the spreadsheet data using JavaScript array methods.
Understanding Data Range
There are a ton of different methods you can use to select values in a Google Sheet, so I’m just going to focus on the easiest one that will work for the most people.
Let’s say we start with a spreadsheet that looks like this:
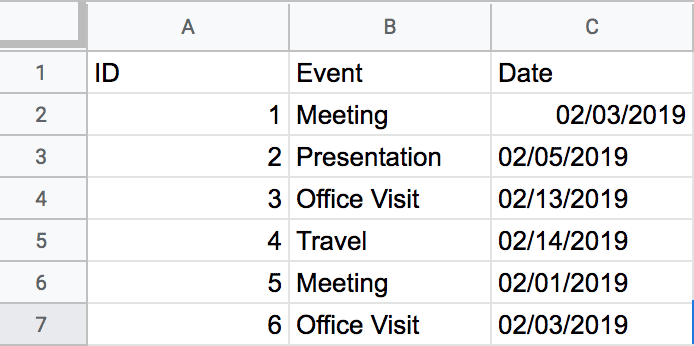
Our data range for this spreadsheet, which means the range of cells in which data is present, is 3 columns wide and 7 columns long including our headers. The concept of data range is important since some rows may not have data in all columns, so blank values will be included where there is nothing present. In other words, if you have 3 rows of data and 15 columns, that will construct the bounds of your data range even if all rows don’t have those cells filled in.
So, how do we do we get all of those values in Google Apps Script?
The following line of Apps Script will access the current active sheet in your spreadsheet, find the data range of your sheet (i.e. the maximum extent of values in cols/rows), and then return those values as a two dimensional array:
var rows = SpreadsheetApp.getActiveSheet().getDataRange().getValues();
The better you understand how to work with arrays in JavaScript, the more sense this data structure will make. At the end of the day, this is what our rows variable looks like after calling the above methods:
rows = [
['ID','Event','Date'],
[1, 'Meeting', '02/03/2019'],
[2, 'Presentation', '02/05/2019'],
...additional rows here
]
The 2D array structure of rows is one outer array that corresponds to the data range of the sheet. This outer array contains an array for each row in the data range. And this inner array contains all of the values available for that particular row.
Accessing Rows and Values using Array Index
The most important thing to know about working with arrays in this context is how to access the items inside of them. Arrays in JavaScript are zero indexed, meaning the first item inside of each array actually has an index of zero, the second item has an index of one and so on:
rows[0] // First row, index zero // ['ID','Event','Date'] rows[1] // Second row, index one // [1, 'Meeting', '02/03/2019']
From here, the process is similar to access the values inside of each row array.
rows[0][0] // First row, index zero // First value, index zero // 'ID' rows[1][1] // Second row, index one // Second value, index one // 'Meeting'
If this seems annoying, it certainly can be. My best advice is that if you find yourself getting a value you don’t expect, double check your array indexes. The good news is that there are other patterns we can use to work with arrays depending on what kinds of things we want to make happen.
Getting Specific Ranges
In addition to using getDataRange().getValues() to get all of the values in the sheet, we can be more specific with the rows we return from these queries using a variant of the getRange method.
For example, if we wanted to only select values from our example table in the first and second columns, excluding the headers this time, we could use an expression that looks like this:
var rows = SpreadsheetApp.getActiveSheet().getRange(2, 1, 6, 2).getValues()
The first and second parameters we pass into getRange represent the top-left of our range (e.g. second row, first column), while the third parameter tells the function how many rows tall the Range will be ( e.g. six rows tall), and the last parameter tells the function how wide the Range will be (e.g. two rows wide).
The values we have stored in the rows variable correspond to this shape in our spreadsheet:
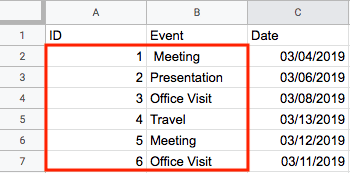
If we log out the value of rows using the last select statement, we get a 2D array that looks like this:
rows = [ [1, 'Meeting'], [2, 'Presentation'], ...additional rows here ]
From here we can manipulate the array however we want using JavaScript to execute additional parts of your program.
A Gotcha with Mental Models of Ranges vs. Arrays
A lot of times when you are programming, you develop a mental model of how a things work together that helps you handle complexity. In Google Sheets and Google Apps Script, you can start to envision the entire spreadsheet as a giant 2D array.
While that is a helpful construct, sometimes it can lead to confusion when things in JavaScript and Google Apps Script don’t correspond. A great example of that is how both JavaScript arrays and Google Sheets apply indexing.
Remember that arrays are zero-index, and a Sheets index starts at 1 for rows and columns. Take a look at this little function, that attempts to get and access the same value using those two conventions.
function getSpecificValue () {
var value = SpreadsheetApp.getActiveSheet().getRange(1, 1).getValues();
var id = value[0][0];
}
In practice, this is a common place for someone to superimpose a value that leads to a lot of frustrated time debugging. If you are getting and reading data from a spreadsheet, and the results aren’t expected, check this place first before questioning your sanity.
Processing Rows of Google Sheets
Now that we have talked about different ways to select Google Sheets rows in Google Apps Script, it’s likely that you want to process them in some way as a part of a large automation.
Some common patterns involve doing something for each entry, or filtering each entry based on a particular condition.
Do Something For Each Row | forEach loop
Once we get all of the rows and values in a spreadsheet, a very common thing is to perform the same operation on all of the rows. Maybe we have a list of clients, and we want to send them all the same templated email (i.e. mail merge type operation), or maybe we have a list of people signed up for a 5K and we want to generate PDF waivers for each of them. The possibilities are endless.
We can fairly easily accomplish this pattern using a forEach loop on the result we get back from the data selection function above.
/****
rows = [
['Jeff', 'jeff@email.com', 'Cool guy...']
]
****/
rows.forEach(function(row) {
var email = row[1];
MailApp.sendEmail(email, 'Hey you!', 'This is the body of the message');
});
The forEach method is super powerful and helpful. For starters, it lets you remove one time consuming step of individual selecting rows using array indices. From there, you just have to worry about passing in the row and accessing the values within each row.
If you need to skip a row or a few based on some condition, we can also do something like this:
/****
rows = [
['Name', 'Email', 'Bio'],
['Jeff', 'jeff@email.com', 'Cool guy...']
]
****/
rows.forEach(function(row, index) {
if (index !== 0) {
var email = row[1];
MailApp.sendEmail(email, 'Hey you!', 'This is the body of the message');
}
});
In the above example, we have a row of headers that we need to skip, so we can pass the index parameter into our forEach loop so that we can write some conditional logic to check if the index is zero, which means we are looking at our header row.
The forEach loop is super powerful, and I imagine most scripts of this type will make use of the forEach loop in some capacity. I’d recommend reading the JavaScript docs above to get a good sense for how it can and should be used.
Filtering Rows that Meet a Condition | filter
Another question I get asked a lot is how to do something when a particular value in a row meets a condition. For example, when filling out an event registration form, I want to send an email only to people who selected ‘Vegetarian’ as the dinner option.
Technically, we could also do that similar to the conditional logic in the example above, i.e. if row[3] === 'Vegetarian', and just execute our code, but that can easily lead to a ton of nested code inside a forEach loop. There is a better array method to filter results out of an array:
/***
rows = [
['Email', 'Number of Guests', 'Dinner Choice'],
['jeff@email.com', 2, 'Vegetarian'],
['someone@email.com', 1, 'Beef'],
['else@email.com', 3, 'Vegetarian'],
]
****/
var filteredRows = rows.filter(function(row){
if (row[2] === 'Vegetarian') {
return row;
}
});
/***
Now, filteredRows looks like this
filteredRows = [
['jeff@email.com', 2, 'Vegetarian'],
['else@email.com', 3, 'Vegetarian'],
]
***/
We call the filter method on our array of rows, and then we pass in a callback function that takes the row as a parameter. Inside the callback function, you check for whatever value you are looking for or not looking for, and return the row if it meets your condition. If you want the row filtered out, just don’t return anything.
From there, we can call forEach on the filteredRows array to do the things we want to do on the subset of rows:
filteredRows.forEach(function(row) {
//Do something here
}
Wrapping Up
There are several other ways to get data out of the spreadsheet that are slightly more complex than what I’ve talked about here, but again this method should work for most people doing most things. If you have a particular thing you are trying to accomplish that these methods might not support, feel free to leave a comment with more details.
hi,
thanks for the tutorial!
i managed to return the rows with certain condition, however how do i perform formatting of that row?
eg setbackground to the row.
i tried row.setbackground(“red”);
i got type error
Thanks for reading and reaching out. I can’t be certain without looking at your code, which you are more than welcome to post here for review, but my guess is they Type error is because using
SpreadsheetApp.getActiveSheet().getDataRange().getValues();gets the values from the Spreadsheet, where you need to call setBackground on a Range object. You can consider a Range a reference to spreadsheet cells, whereas the values are what is inside of them.So, if you wanted to change the background on the entire data range, just create a variable called
var range = SpreadsheetApp.getActiveSheet().getDataRange();and then call setBackground on that. If you want a more specific range, you can use one of the methods like getLastRow to find a particular range.Thanks for reading. Feel free to post back with more questions or a code sample, which always helps.
Hi
Thanks for the tutorial.
I am trying to implement a piece of code that will send an email, with information from a row. That row is only selected if data in a row matches a condition.
Currently my code script is as follows:function Due_Date() {
//Date Info
var One_Day = 1000 * 60 * 60 * 24;
var Today = new Date();
var Warning_Date = new Date(Today.getTime() + (One_Day * 4));
var DataSet = SpreadsheetApp.getActiveSpreadsheet().getSheetByName(“Brand & Upweight”).getDataRange().getValues();
//Get Due Date Data
var filteredDataSets = DataSet.filter(function(row){
if (row[2] = (Warning_Date -4)) {
return row;
// Fetch the email address
var emailRange = SpreadsheetApp.getActiveSpreadsheet().getSheetByName(“Brand & Upweight”).getRange(“B1”);
var emailAddress = emailRange.getValues();
// Send Alert Email.
var message = ‘Just a heads up that we have content that is due in four days! Go look at the calendar to see what it is.’; // Second column
var subject = ‘Content is due!’;
MailApp.sendEmail(emailAddress, subject, message);
}})}
How would I go about getting the information from the returned row into the email?
Any help would be smashing
Thanks for reading and leaving a comment. First off, I notice in your filter function you are using a single equals sign
=, which is used to assign a variable in JS, and not the double or triple equals== || ===, which EVALUATE equality or strict equality. I’d recommend reading this article on equality to learn more. Since you aren’t comparing anything, none of the code in the if block gets run.Second, assuming you fix the equality issue above, you return the row and then execute some additional code. Using the
returnstatement inside of a function means that nothing after it will get run. Returning effectively ends the execution of that function, which is all we want to do inside of a filter loop.To do what you are asking, I would remove all of the logic below the return statement so that all the filter loop does is generate a new array of data called
filteredDataSets. After that, you can use theforEachmethod to loop over your filtered array and call the code to send each email, something likefilteredDataSets.forEach(sendEmail(data)).Whew! That is a lot to write in one comment reply, so be sure to write back if you have any questions. Thanks for reading.
Jeff
Hello, excellent tutorial!
I am trying to implement a code to save and read values by pointing to the column name (the value found in the first row) and the row according to a key Id (Value found in the first column) in order to use it as an application web, so that it allows me to have several sheets in the same book and access all the information using as parameters the name of the sheet, the name of the column, the Key Id of the row and the value to Save / Read / Delete .
But I am confused, after reading row [0], how should I do to associate it with the column index?
Thank you in advance
That’s a very good question, so thanks for asking. The tricky part is how JavaScript treats arrays vs. how Google Sheets treats Range object within a spreadsheet. JavaScript arrays use zero indexing, while all references to spreadsheet ranges start at 1.
So, for example, the first column of the first row in a JS array returned by getDataRange().getValues(), would be accessed like this: array[0][0].
However, if we wanted to select that range using Sheet.getRange we would access that same cell like this: Sheet.getRange(1,1). Once you have the range as a variable, you can call Range.setValue() on that range to update the cell.
Essentially, to map array values to sheet ranges, it is just the array index (whether row or column) + 1 to get the corresponding range. Hopefully, that helps answer your question, but if I missed the mark here please comment back in this thread and we can work through what you are trying to do.
Thanks for reading!
Regards,
JE
Hi, I am using below app script to retrieve a set of filtered values from a google sheet. I am supplying mobile number from an HTML page and passing that to below function. Everything is working fine, but my fetching of data is taking 4 – 5 seconds. I have only 300 rows in the sheet and each filtered dataset is hardly 4 -5 rows. How do I improv the speed of fetching data.
function getTravelDet1(emp){
emp=Math.round(emp)
ssID=”1IMqTbZ4shxE6YBKgZB5fQcvUdiGSE-XSnHfoFSCdxOo”
ssSheet=SpreadsheetApp.openById(ssID).getSheetByName(“aprView”);
data=ssSheet.getRange(1, 1, ssSheet.getLastRow()-1, ssSheet.getLastColumn()).getValues();
var filteredRows = data.filter(function(row){
if (row[0] === emp) {
return row;
}
});
return filteredRows;
}
Sorry for the late reply.
The only thing I can really think of is to limit the amount of data selected on the initial query. For example, perhaps you could get just the range that contains the number you are filtering for, so one column on all the rows. Then, you could filter that to determine what rows to get, then get just those rows. That would prevent you from having to load all of the 300 rows into memory.
You could also do some profiling to see where things are slow. If you log some timestamps at different parts of the procedure, you could see which part takes the longest. That would at least tell you objectively where your procedure is slow.
JE
Hi, very well written understandable tutorial. Here is my problem for my school student library.
* Transaction Sheet has 3 columns (memberid, bookid, action[borrow/return]) which are updated by a Form.
* Catalog Sheet has 3 cloumns (bookid,bookname,status).
Now when a user fills the form (m001,b001,return) a row will be added to Transaction.
What i want is : As that book b001 is returned, in Catalog Sheet, b001 row’s status should change from ISSUED to AVAILABLE automatically. Please help me out.
Hi Kamal, that sounds like a pretty interesting problem. You will need to intercept the form response to get the bookid, then find where bookid is listed in the ‘Catalog Sheet,’ then update that range. Here is just a quick code sketch to get you started:
function returnBook(e){
var bookid = e.values[1];
var action = e.values[2];
if (action === 'return') {
var catalogSheet = SpreadsheetApp.getActiveSpreadsheet().getSheetByName('Catalog Sheet');
var books = catalogSheet.getDataRange().getValues();
var returnedBookIndex = null;
books.forEach(function(book, index){
if (book[1] === bookid) {
returnedBookIndex = index;
}
})
if(returnedBookIndex) {
catalogSheet.getRange(returnedBookIndex + 1, 2).setValue('AVAILABLE')
}
}
}
Hello!
I am looking to remove a drop down selection on a form based of responses from said form. Once that response reaches a maximum number of responses, it is then removed from the form.
The issue I run into with this above tutorial is I cannot figure out how to filter out blanks? I have the list of responses in a spreadsheet, and once they reach a maximum response limit, the cell they are in goes blank. However, when trying to populate that range into the form, I get an error for having an empty cell within that range on the form questions. So I’d like to be able to filter out the blanks from that range to be able to remove them from the drop down list.
Thanks for this tutorial and you help!
Hey Tim,
Can you perhaps log some of the data using the Logger.log method so we can inspect it?
I have a tutorial here on debugging that could be helpful. If you can show the me that data as an array when you retrieve it from the sheet, I should be able to help you write a filter function to remove the rows you are looking for.
Also feel free to post the code that makes the modifications to the Google Form since some of that might be relevant.
Thanks for reading,
Jeff
Hi, thanks for the clear and thorough explanation! but i have a bit problems, how do i got array of data from another file/spreadsheet? is it possible?
Hi Nadhif,
Thanks for reading and reaching out. You should be able to get the data from any spreadsheet by referencing it using SpreadsheetApp.openById method:
var otherSheet = SpreadsheetApp.openById('id goes here');
var data = otherSheet.getDataRange().getValues();
Let me know if that doesn’t help you with this issue.
Thanks,
Jeff
Hi, I don’t know if you are still monitoring this, but I used the code in the example above and I return a single row as planned from the sheet in filter rows.
The script has placed all of the columns at index zero, comma-separated. Therefore if I log filteredRows[0] I get all of the data. if I log filteredRows[1] I get null.
There are twelve columns. Any ideas what is casuing this?
Hi. User error. I was not indexing [0][1]!
Awesome! Great that you caught it. Thanks for reading!
JE
rows.forEach(function(row, index) {
var isitreallyBlank = row[5].isBlank();
})
Not sure why but an error message .isBlank() not a function popped out…
Hi,
Sorry for the late reply. That function only exists on a Range object, not on the values inside of that Range, which is what we extract into the rows variable.
https://developers.google.com/apps-script/reference/spreadsheet/range#isBlank()
There are other ways to test the ‘truthiness’ of those values just using JavaScript.
Thanks for watching/reading,
Jeff
Thank you very much – just getting into Apps Script and I was finding very difficult to get to know how get data out of the sheets and into an array. Luckily I stumbled across this information and it’s perfect. Brilliant!! Thank you Again!
Hey Ian, Always great to hear that from someone starting out. Glad this could be of help, and thanks so much for the kind words. Cheers, Jeff
This was really helpful, but I had a specific question. I am just learning JS and Google Script. I have a single column of URLs, and I am trying to use getValues() to create an array that I can then use fetchAll() to fetch the URLs then getContentText() and then MatchAll(). The thing I can’t figure out is that getValues() creates a 2D array, but fetchAll() needs a 1D array. How do I convert or flatten the 2D Array to a 1D array?
This is a great question and a good use of the Array.map method in JS: https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Array/map
Essentially, you iterate over the first array and return a new value for every element in the original array. So, something like this would work:
const newArr = oldArr.map(values => values[indexOfUrl])Thanks for reading! Jeff
I am getting this error from the first step from your video.
ReferenceError: logger is not defined
useDataRange @ Code.gs:3
The Logger class is defined using ‘Logger’ with a capital ‘L’
Thank you. This article was very helpful.